Cómo determinar el valor de una notación científica.
Vamos a centrarnos en la parte que nos interesa, que es la de la electrónica. En algunas ocasiones cuando queremos utilizar un condensador de los que tenemos guardados en un departamento de material usado o de los que acabamos de adquirir en el comercio, nos encontramos en un pequeño dilema, se trata de saber el valor de unas siglas que por no ser habituales, nos pueden llevar a confusión o error de interpretación.
Todos sabemos que el valor de los condensadores casi siempre viene expresado con submúltiplos del Faradio ya que éste, es una unidad muy grande y normalmente está fuera de nuestro uso. Por tanto, cuando por medio de cálculos, llegamos a la situación de interpretar el valor de un condensador, en primer lugar debemos considerar si se trata de un condensador polarizado, en cuyo caso los valores suelen estar comprendidos entre 0,1µf a varios miles de microfaradios, raramente se superan los 800.000 µf, últimamente en algún equipo de vídeo o similar, se puede ver en lugar de una pequeña batería, un condensador electrolítico de 1F o poco más a unos 5V, esto como digo son casos muy especiales.
En cuanto a los que no son polarizados, los de mayor capacidad son los MKT, MKP, Tántalo y luego están los más comunes condensadores cerámicos que suelen estar comprendidos entre los pocos microfaradios y los nanofaradios y es en este caso cuando entra a formar parte del problema el interpretar el valor del mismo.
Por lo tanto, para pedirlo en el comercio que habitualmente visitamos. Veamos el condensador de 0,000047 F (Faradios), cómo lo pedimos al dependiente de la tienda, existe la posibilidad de error. O, al leer el código de colores de un condensador que hemos adquirido y pasarlo a números.
¡Este es el método!, sigue leyendo.
Para salir airosos de una situación como esta, debemos recurrir a una estrategia o método sencillo y fácil de recordar (de que me suena esto, ‘Cuando no encuentres una solución, vuelve a lo básico, a lo que conoces bien‘), si hacemos caso a este proverbio, qué es lo básico en nuestro problema, las subdivisiones de una medida y cómo enfocamos el problema. Veamos:
-
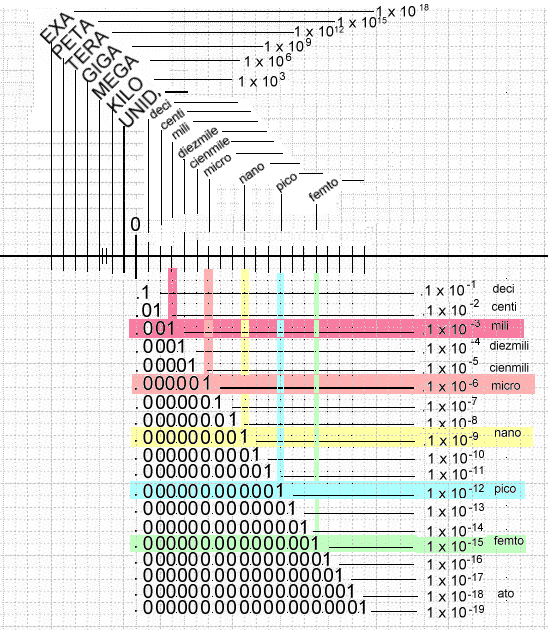
Trazar una línea horizontal de cierta longitud, a la cual dividiremos con unos doce trazos verticales más o menos equidistantes entre sí, como se muestra (tampoco es necesario trazar todo lo que aparece en la siguiente fig. 1 ) que sólo es una muestra. Puedes usar una hoja cuadriculada de una libreta.
Nos centraremos en lo que se encuentra a la derecha del 0. Ahora es cuestión de seguir un sencillo proceso para averiguar el valor de la medida en cuestión. Por cierto, la anotación decimal, sigue la reglas europeas.
He resaltado con diferentes colores los tópicos más utilizados. Unos ejemplos nos darán la práctica necesaria para dominar el funcionamiento del sistema.
-
Tenemos el siguiente valor en el cuerpo del condensador: 0,0015 F. El primer paso es contar el número de dígitos detrás de la coma decimal,
0,0015 – valor en el cuerpo.
0,000001 – en la regla, lugar más cercano.
0,001500 – lectura del valor, 1.500 µf
Creo que esta forma de presentarlo es la más sencilla, véase la estrategia de añadir ceros detrás del último dígito del condensador en este caso el 5, de forma que completamos hasta la columna que más nos acerque al decimal con la fila que se corresponda en la de la figura 1, podemos observar que se trata de diezmilésimas y entonces diremos que se trata de un condensador de 1,5 centésimas de faradio, término que no es muy usado, lo más común es 15 mF (15 milifaradios o 15 milésimas de faradio), en notación científica 1,5 x 10-3 (10 elevado a -3). El término más utilizado es 1.500uf (mil quinientos microfaradios).
-
Otro caso, ahora, el desarrollo matemático realizado nos ha dado un resultado de 0,00000047 F (Faradios). El primer paso es, contar el número de dígitos detrás de la coma decimal, en este caso son 8, como el valor más cercano (por exceso en este caso) es el de elevado a -9, lo comparamos y nos proporciona el valor de 470 nanofaradios.
-
En el caso de un condensador de 20 µF. Si estamos hablando de ‘micro’, esto significa que detrás de la coma hay que ocupar 6 dígitos, veamos:
0,000001 – corresponde a 1 microfaradio, por lo tanto
0,000020 – µF, que es su representación. -
Finalmente tenemos la siguiente notación 0,0000001 F. Al comparar con la fila correspondiente de la figura, vemos que rebasa en uno los µF (microfaradios), por lo que le añadiremos dos ceros detrás del 1 y por fin tendremos 100 nF (100 nanofaradios), que es el siguiente submúltiplo, el nanofaradio. Véase la tabla de equivalencias entre valores en la figura 2.
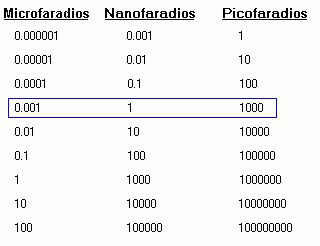
En esta imagen que presentamos a continuación, puede ser muy eficaz a la hora de entender estas subdivisiones que a muchos llevan de cabeza.
Como siempre con un ejemplo se aclaran las ideas. Hemos trazado un rectángulo que abarca una línea de la figura 2. Cómo haría para que se entienda… creo que ya lo tengo. Imaginemos que tenemos 1000 pf, lo que es lo mismo que 1 nf y por lo tanto 0’001 µf, como se puede apreciar en la línea resaltada. Ahora creo que está más claro. En general, por si hubiera alguna dificultad en comprender lo que he descrito, a continuación presento una tabla de las abreviaturas, algo más completa, la cual espero se entienda mejor.
Nota:
Algunos tipos de condensadores tienen marcados los valores en diferentes unidades. La tabla anterior nos ayudará a convertir entre estos valores. Los valores de estas unidades son:
| Mili = 10E-9 | <=> | Micro = 10E-6 |
| Nano = 10E-9 | <=> | Pico = 10E-12 |
Estos condensadores vienen marcados utilizando códigos de tres dígitos, similar al utilizador por las resistencias.
-
En los condensadores cerámicos, los valores siempre vienen expresados en picofaradios (pf) impreso en números y dados por tres cifras cuyo valor está determinado por su posición relativa.
-
De esta forma las dos primeras cifras de la izquierda, corresponden al valor numérico significativo de su capacidad, siendo la tercera cifra (la de la derecha), la que expresa el número de ceros que se deben agregar a las dos cifras anteriores, lo que nos dará la correspondiente capacidad en picofaradios.
Lo más típico según lo anterior es, encontrar condensadores con números con anotaciones compuestas por una serie de 3 cifras y una letra.
Por ejemplo sea: 473Z
Primer número: 4
Segundo número: 7
Tercer número: 3 = 000
Cuya capacidad es de 47.000 pf o 47 nf o también 47k, donde la Z corresponde a la tolerancia entre el +80% y -20%, ver fig. 2 la tabla de equivalencias entre valores.
Espero que con estos ejemplos haya quedado clara la forma de utilizar estas tablas, no obstante si necesitas alguna aclaración, ponte en contacto con migo