Lógica secuencial.

Los circuitos de las aplicaciones estudiadas hasta ahora, se consideran pertenecientes a la lógica combinacional, en la que sus componentes proporcionan una salida, que es siempre dependiente de los estados de sus entradas. Tantas veces como se repitan los estados en las entradas, así, se repetirán las salidas, presentando los mismos resultados previstos. 

En cambio, en los sistemas pertenecientes a la lógica secuencial, sus salidas no dependen únicamente de los estados de las entradas, además, dependen de estados producidos por secuencias anteriores y que han sido memorizados, algunas veces por ellos mismos.

Este tipo de lógica secuencial que acabamos de indicar comprende el estudio de sistemas en los que aunque se repita la combinación de los estados de las entradas, la salida puede ser diferente, dependiendo de la secuencia/s de cuando y cómo se hayan producido los estados anteriores, lo que se puede llamar, su historia.

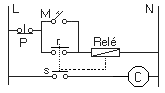
Automatismo practico secuencial.

Así pues, cualquier automatismo industrial, para su puesta en marcha, requieren de un pulsador M y para su parada otro pulsador P. De modo que pulsando por un momento M, se pone en marcha y aunque pulsemos de nuevo o se deje de pulsar M, el automatismo sigue en activo. Para pararlo será necesario pulsar por un momento el pulsador de parada P, que lo desactivará de forma definitiva. 

Este automatismo eléctrico requiere de un relé que dispone de dos contactos. Uno, nos proporciona el estado de retención de la orden de puesta en marcha y el otro por supuesto, se encarga de cerrar el circuito que controla la carga del automatismo.  La figura 7-1, nos muestra el esquema del circuito eléctrico que cumpliría estos requisitos.

Fig. 7-1

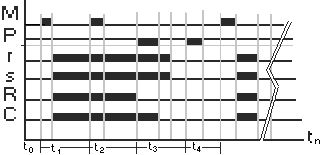
Cuando pulsamos M se activará el relé, y entonces, éste, cierra sus dos contactos r y s, que normalmente están abiertos (NO), por este motivo mediante s, se activa la carga C, a su vez el contacto r se cierra y retiene el paso de corriente de alimentación del relé, permaneciendo en este estado (función memoria), mientras no se pulse el contacto de parada P (NC). En cuyo caso la corriente que mantenía activo el relé, desaparecería y el contacto r se abriría, así como el s, permaneciendo en este estado mientras no se vuelva a pulsar M. 

Para comprender el funcionamiento de este montaje, proponemos un diagrama de tiempos como el mostrado en la figura 7-2. En el que, se puede deducir que mientras que el contacto perteneciente a P se encuentre en reposo (NC), cuando se pulsa M, todos los elementos se activan, el reten del relé r y el contacto de servicio s, a sí como la carga C, que se activará.

 Fig. 7-2

Para los más familiarizados con las tablas de verdad, aquí se presenta la tabla que corresponde al mismo circuito, en la siguiente tabla.

Finalmente podemos concluir diciendo que, a 'priori' no es posible determinar el estado de la carga, con la única información que nos proporcionan ambos pulsadores aunque estén en reposo, caso muy normal, por otra parte.

Segundo automatismo secuencial

 En este segundo ejercicio, mediante la función memoria de los relés R₁ y R₂, debemos poder accionarlos en las siguientes secuencias:

1.- El relé R₁, debe activarse y desactivarse con independencia del relé R₂.

2.- El relé R₂, única y solamente se podrá activar cuando R₁ esté activo.

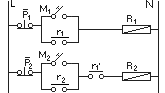
Por el enunciado se deduce la independencia entre R₁ sobre R₂, al primero R₁ lo excitaremos con la simple función de memoria que ya estudiamos en las lecciones teóricas con puertas y en la anterior práctica.

Recordemos, la función memoria, consiste en dotar al sistema de una realimentación que mantenga el circuito en las condiciones de normal funcionamiento. Es lo que ocurre cuando; al pulsar M₁, en la figura 7-1, se activa la bobina R del relé, lo que a su vez hace cerrarse al contacto abierto r (r de retén, por consiguiente la realimentación) y también el contacto s que se encarga de mantener el paso de corriente que pide la carga C.

Sigamos, usaremos la función memoria, intercalando un pulsador de 'borrado' (observar el significado de la palabra 'borrado'), para poder parar el sistema.

R₁ = P₁ (M₁ + R₁)

Dado que R₂ únicamente se activará cuando lo esté R₁, la mencionada función memoria la insertaremos en serie con la condición de que esté R₁ activado. Los mencionados contactos de los relés serán normalmente abiertos (NO, del francés Normalment Overt). En resumen que R₂ será igual a 1 cuando R₁ sea igual a 1.

                
R₂ = P₂ (M₂ + R₂) · R₁

Observar que por la condición Y (AND), R2 no podrá ser igual a 1 mientras que R1 no valga 1. Según estas dos funciones podremos trazar el circuito correspondiente, ver fig.7-3 y comprobar sobre el mismo que se cumplen las condiciones establecidas en el enunciado.

 Fig. 7-3

Si observamos la anterior figura detenidamente podemos apreciar que con unos pocos cambios en la misma, podemos reducir dos contactos. Intente el lector dar la solución sugerida, si no halla la pretendida solución, pase el puntero del ratón sobre la fig. 7-3, para ver la solución.

Tercer sistema secuencial

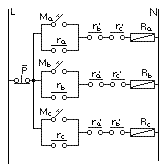
En este caso vamos a controlar tres motores, mediante la función memoria de sendos relés Ra, Rb y Rc que de forma que se cumpla la siguiente condición:

1.- Al poner en funcionamiento cualquiera de los tres motores, se evite la puesta en funcionamiento de cualquiera de los otros dos.

2.- Sólo se dispondrá de un pulsador de parada.

Las tres funciones de memoria, en principio deben ser idénticas y dependerán de un único pulsador de parada P, según nos piden.

         
Ra = P (Ma + Ra)
         
Rb = P (Mb + Rb)

Rc = P (Mc + Rc)

Dado que la principal condicionante es que cuando uno de los relés, esté activado, se impida la activación de cualquiera de los otros dos relés, lo que deberemos hacer es, agregar en serie con cada función de memoria (anteriores) una inversión de cada contacto de los otros dos relés. Es decir, a Ra le insertaremos un contacto invertido de Rb y Rc, así, a la función Rb le insertaremos una inversión del contacto Ra y Rc y por supuesto en serie a Rc le añadimos una inversión de los contactos Ra y Rb.

                               
Ra = P (Ma + Ra) Rb' Rc'
                                      
Rb = P (Mb + Rb) Ra' Rc'
                                
Rc = P (Mc + Rc) Ra' Rb'

Ahora, es sencillo deducir el circuito eléctrico que cumpla estas tres funciones. Analicemos el esquema descrito en la figura 7-5. Supongamos que Rc es activado o sea, Rc = 1, por lo que Ra' y Rb', en serie con Rc, hace que las otras dos funciones no puedan ser activadas debido a que en ellas están multiplicadas Rc × Ra' × Rb' o sea la función AND.

Fig. 7-5

Cuarto automatismo secuencial

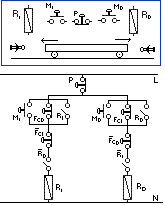
Necesitamos proyectar un sistema automático de vaivén, algunas máquinas , como el carro de una máquina cepilladora. Dicho automatismo responde a los siguientes requisitos:

1.- El movimiento de vaivén debe poder iniciarse, en uno u otro sentido, por medio de Md y Mi.
2.- Por medio de dos finales de carrera Fcd y Fci, se limitará el recorrido, en uno u toro sentido, lo que indicará el inicio del sentido contrario. 
3.- Un pulsador de parada P, permitirá detener el movimiento, sea cual sea su estado, sentido y posición del carro.
4.- El proyecto dispondrá de un sistema de seguridad que impida que ambos motores funcionen simultáneamente. 

Con el fin de clarificar el desarrollo del proyecto y sus funciones lógicas expuestas, dispondremos de un diagrama de los elementos descritos (enmarcado).

La función de marcha a la derecha Md con el relé Rd sería así:

R_D => (M_D + R_D)