|
|
|
LECCIÓN 7 LECCIÓN 8 LECCIÓN 9 LECCIÓN 10
|
|
PRÁCTICA DIGITAL
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
En las lecciones anteriores hemos tratado la teoría que tanto suele agobiar a la mayoría y en la última lección con estos conocimientos, entramos a dar solución a unos problemas que se presentaron. Cuanto menos tendremos que reconocer que la teoría está más que justificada ya se vio lo importante que resultó a la hora de simplificar las ecuaciones. En esta lección, veremos:
En la resolución de los problemas y funciones lógicas, además de la suma, producto y negación, existen otras operaciones que se derivan de estas tres mencionadas, los cuales son de práctica aplicación en la mayor parte de las operaciones ya que ayudan a reducir enormemente las ecuaciones, nos estamos refiriendo a los operadores NOR, NAND y OR EXCLUSIVA. Este operador o puerta NOR (del ingles No OR), es producto de la inversión de la suma. Es decir, de las variables (también conocidas como conjuntos), A, B y C produce a su salida como resultado: A+B+C Veamos la tabla de verdad que corresponde a la operación NOR de las variables A, B y C.
Tabla de verdad de una
puerta El símbolo del operador lógico que se utiliza en los esquemas lógicos, pertenece a la suma seguida de la inversión y se representa por el símbolo de la suma unido a un pequeño círculo que representa la inversión. Véase la figura 5-1.
Obtención de un inversor con una una puerta NOR Es sencillo obtener un inversor mediante un operador NOR, al contemplar la tabla de verdad de éste, podemos comprender que en el momento que unimos todas las entradas y aplicamos un nivel lógico en la entrada común en la salida obtenemos el mismo nivel pero invertido.
Tabla de verdad Y el símbolo del inversor con un
NOR. De igual manera se puede obtener una suma con operadores NOR. De hecho, lo que ocurre con una puerta NOR es la negación de una suma, como ya se ha demostrado, bien, este es el caso, cuando realizamos una doble negación, que ocurre, simplemente se obtiene una inalteración de la variable de entrada, como se aprecia en la figura 26.
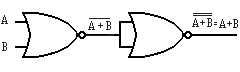
Esta es la forma más sencilla de obtener una suma sin negar, introduciendo las variables en una NOR y su salida a las dos entradas del siguiente. El producto con puertas NOR Según uno de los teoremas de Morgan, expresa que la negación de la suma de dos variables es igual al producto de la inversión de cada una e ellas, ver función siguiente. (F. 1) A+B = A ·B De esta igualdad se entiende y deduce que la suma negada de dos variables es igual al producto de las variables, cada una negada por separado. El símbolo lógico para tres entradas, se puede ver en la figura 5-1. También se puede demostrar el teorema de Morgan si aplicamos las variables invertidas en las entradas, ver la figura 5-4:
Operaciones con operadores NAND Ahora vamos a estudiar las posibilidades de operar y cómo realizar las operaciones con los operadores NAND. Si aplicamos una variable a una entrada única de un operador NAND, a la salida obtendremos la inversión de dicha variable de entrada. En esto naturalmente no hay diferencia con respecto a lo obtenido con una puerta NOR, por lo tanto nos sirve la imagen de la figura 5-2, sólo que con un operador NAND.
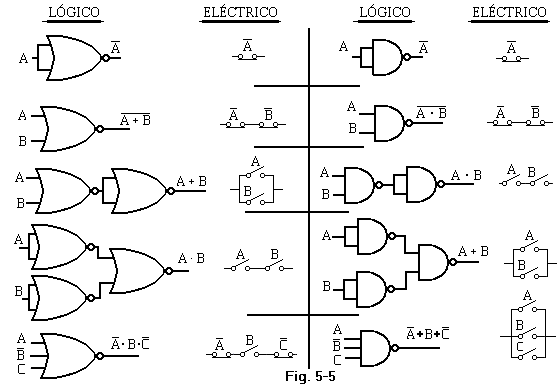
A continuación, presentamos la figura de la derecha, que resume lo expuesto en estos párrafos. Se ha demostrado la posibilidad de efectuar todas las operaciones de la teoría expresada en el álgebra de Boole mediante puertas NOR, de la misma forma se pueden expresar dichas operaciones con la aplicación de puertas NAND, para no profundizar de alguna manera en lo expuesto con las puerta NOR, nos remitiremos a la mencionada figura 5-5, donde se muestran las equivalencias como resumen de todo ello.
Estas operaciones contemplan la combinación de las expresiones con puertas NOR y NAND, para la resolución de los problemas, mediante la reducción de las funciones por medio de los diagramas de Karnaugh para dos o más variables. Pero no vamos a entrar en la parte de la teoría, ya que no es nuestro cometido, entendemos que la teoría ya descrita y la práctica pueden aclarar los conceptos que nos interesan. Si alguien está interesado en profundizar sus conocimientos sobre el tema, es el momento de adquirir algún libro, de la extensa librería que habla del tema y empiece su ampliación de conocimientos. Si repasamos lo que hemos aprendido, deberíamos plantear la tabla de verdad de cualquiera de las funciones, bueno puertas lógicas que representan a aquellas, sin ningún problema. Recomiendo que haga muchas prácticas con los planteamientos de los problemas expuestos y los que a Ud. se le presenten en su día a día y trate de resolverlo, verá que es cuestión de ponerse a ello. Un secreto, si un problema se le resiste, no dude en partirlo en otros problemas más sencillos y naturalmente resuelva cada uno de ellos y verá que tiene el gran problema resuelto. Esto, no es mío, pero funciona. Ha llegado el momento de la práctica y sin embargo nos asaltan las dudas, pero esté tranquilo, ya sabemos que este no es un sistema de estudio muy ortodoxo, pero estamos convencidos que no perdemos de vista lo más importante que es aprender y la naturaleza en su mayor parte nos muestra cómo se sirve para que aprendamos, que cómo lo hace, con el método de error y corrección y por ahí van los pasos que andaremos si nos acompaña por este maravilloso itinerario digital.
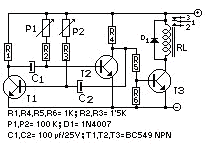
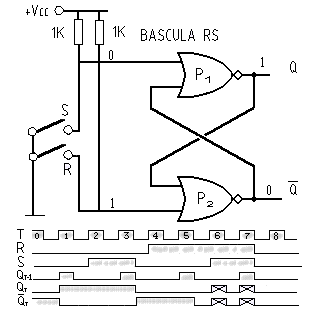
En muchos casos cada día nos encontramos por todas partes con los conocidos anuncios luminosos que parpadean todos ellos utilizan un, más o menos elaborado, conmutador electrónico (biestable) que se encarga de cortar la tensión de alimentación por un tiempo preestablecido para lograr el efecto deseado. Pues bien, este (mal llamado en este caso) conmutador, si lo imaginamos veremos que se comporta como un biestable o sea, que oscila en un estado se enciende y en otro estado se apaga, y como los tiempos de cada estado, se pueden cambiar y hacer muy cortos o largos, estamos ante un biestable. Este es el nombre más común para este sistema de 'parpadeo'. Veamos cómo actúa el biestable (dos estados), bueno vamos a considerar que los cambios son bastante largos y que tenemos un sistema que en un estado, enciende una lámpara digamos roja y en el caso de estar apagada, el mismo sistema nos encienda otra lámpara verde, por ejemplo. Que esta sucediendo, que esto se comporta como una báscula, exacto una se enciende mientras que la otra permanece apagada. Un ejemplo de una báscula se puede ver en la figura 2, del manual del circuito temporizador, descrito en ua555 donde se describe el funcionamiento del biestable como temporizador. Por lo tanto, podemos ver el biestable o multivibrador como una capacidad de la báscula.En esencia en la figura 5-6, podemos apreciar una versión de una báscula realizada con dos transistores y unos pocos componentes convencionales y en la figura 5-7, una báscula realizada con puertas lógicas NOR. Aun, no siendo lo mismo, el principio de funcionamiento, si es el mismo, aunque la tecnología empleada sea un tanto diferente.
Las diferencias físicas se pueden obviar aunque ambos tienen su particularidad. En la primera se utilizan muchos componentes pero tiene más robustez en cuanto a que activa directamente un relé a su salida si es el caso, por contra tiene más consumo, es menos rápido. Observemos que en la fig. 5-7, que representa una báscula del tipo R-S, hemos añadido el diagrama de tiempos, en donde T, es el factor tiempo o impulsos de reloj, R es una entrada la cual siempre debe estar en oposición al estado de S que, es la otra entrada, esto lo logramos con la ayuda de dos interruptores o pulsadores, debemos percatarnos de las dos resistencias de 1k conectadas a cada una de las entradas y ambas al polo positivo de +Vcc, esto nos proporciona un estado alto (H) en cualquier entrada 'flotante', es decir, aquella entrada que por uno u otro motivo está al aire, evitando un estado de indeterminación. El estado representado por Q T-1, es el estado de transición entre dos cambios de posición consecutivos de los interruptores. En la misma figura 5-7, se puede observar la incoherencia que presenta este tipo de básculas R-S (R-S, por lo de Reset-Set). Analicemos:
Este pequeño inconveniente se podría paliar en parte, cambiando los dos interruptores por un único conmutador de dos posiciones, conectando el común a masa. Este es el motivo por el que se buscó una manera de formar una báscula que no tuviera estos inconvenientes, apareciendo los conocidos tipos Básculas D. las del tipo T y los J-K, al mismo tiempo se apreció la conveniencia de dotarles de una particularidad, la de poder dispararles con el flanco de subida o el flanco de bajada, que ya estudiaremos más adelante.
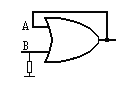
El elemento básico de memoria, la interconexión entre puertas AND y OR como las visto anteriormente, pueden ser conectadas entre si para formar elementos de memoria las cuales tienen la capacidad de 'recordar' si a sus entradas se aplicó un nivel lógico 1 en un momento anterior dando como consecuencia un estado 1 a su salida. Es conveniente practicar cómo se comportan las células de memoria y las puertas (toma de decisión), porque, es difícil comprender cómo se puede acordar una puerta del nivel que se aplicó a su entrada. Empecemos por analizar la expresión mínima de una célula de memoria formada por una puerta OR, ver la figura 5-8.
Podemos comprobar que en principio que la salida S de esta puerta, se encuentra a nivel 0, como la entrada B, la resistencia a masa se aplica para evitar oscilaciones indeseadas que den un estado indeterminado a la salida. Dado que la salida S está a nivel 0 es evidente que la entrada A estará a 0 por estar interconectadas entre si. Cuando aplicamos un nivel 1 en la entrada B de una puerta OR, ésta nos presenta un nivel 1 a su salida y en nuestro caso, acto seguido este nivel 1 se aplica a la entrada A, que ocurre si en la entrada B aplicamos un nivel 0, no ocurre nada en absoluto, ya que la salida le aplicó un 1 a la entrada A y este nivel 1 sigue por siempre dando un 1 a la salida. Para devolver al estado inicial a esta célula de memoria, o bien se corta la alimentación o se corta la unión entre la salida S y la entrada A, no hay otra forma. ¡Eso es memoria!
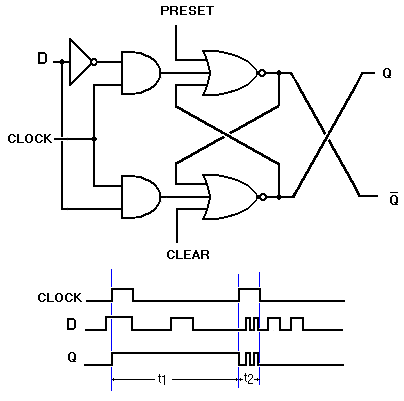
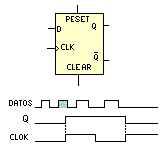
La báscula D, sólo tiene una entrada de datos y debido a que se ha aplicado un inversor entre las entradas R y S éstas siempre estarán en oposición, lo que evitará la posibilidad de indeterminación, además se le ha dotado de una entrada de señal de reloj. Observamos que la salida Q = 1, cuando en la señal de reloj está a nivel lógico 1 y al mismo tiempo D = 1. Pasa a Q = 0 cuando haya caído D a 0 lógico y simultáneamente la señal de reloj pasa de nuevo a 1, es decir, la salida se presenta con el nivel alto de la señal de reloj, lo que se llama en el flanco de subida del reloj. Veamos la figura 5-8.
Como vemos la báscula D es una modificación de la báscula R-S, que mediante un inversor intercalado entre sus entradas R-S, elimina la posibilidad de indeterminación que presenta aquella. El circuito de un flip-flop tipo D, es algo más que el circuito de una báscula D, aunque parece muy similar, también tiene una única entrada de datos y una de reloj. Es bastante más complicado, la diferencia básica está en la nueva forma de utilizar la señal de reloj. A veces en los circuitos digitales, interesa asegurar que no pueda cambiar un dato de entrada durante el intervalo de ser transferido ese dato a la salida y se utiliza la técnica de 'flanco de disparo'. Por consiguiente, llamaremos báscula a los elementos que utilicen el nivel activo de reloj y flip-flop a los que utilicen el flanco de subida o disparo. Un flip-flop D, está constituido por dos básculas como entradas y una tercera báscula para la salida. Las básculas de entrada están interconectadas entre sí de forma que, al llegar el nivel bajo al nivel alto la señal de reloj, produce los estados complementarios en la entrada de la báscula de estados complementarios.
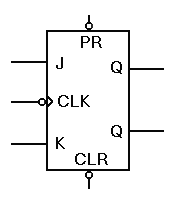
Nota. Las entradas negadas en los símbolos, generalmente se representan con un pequeño circulo junto al cuerpo del símbolo. En este caso, el dato se transferirá a la salida y se indica con el circulo por el flanco de bajada del CLK. Para conectar los flip-flop J-K, disponemos de dos formas de configurar su activación:
El flip-flop J-K, actúa como se indica: si una de sus entradas tienen un nivel lógico 1 y la otra un nivel lógico 0, la salida Q se pondrá a 1 o a 0 con el flanco de bajada de la señal de reloj y permanecerá en este estado de salida, al igual que ocurre con la báscula R-S. Si ambas entradas están a nivel lógico 0, cuando lleguen los impulsos de reloj no cambiará, sin embargo si sus dos entradas están a nivel lógico 1, el flip-flop cambiará sus salidas con cada bajada del impulso de reloj; esto es lo que se llama trabajar en modo 'balanceo' (toggle en inglés). Este modo de trabajar es debido a que los niveles de las entradas J-K, se almacenan durante el transito del impulso de reloj, no cambiando durante ese tiempo su estado el biestable, una vez llega el siguiente flanco de bajada es cuando los datos almacenados hacen balancear el flip-flop. Resumiendo, el funcionamiento del filp-flop J-K (maestro-esclavo), cuando J=K=1, invierte el estado de las salidas Q y /Q en cada impulso de la señal de reloj.
Si alguna cuestión no ha quedado clara se
recomienda visitar la práctica 3 donde se proponen unos ejercicios para
mejor comprensión, en otro caso, deberías indicármelo en
este enlace
|


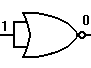 Fig. 5-2
Fig. 5-2
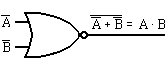
 De igual forma nos ocurre con el producto de dos variable
invertidas que estudiamos en la función (F.1). La particularidad de un operador
NAND reside en que, si una de sus entradas se pone permanentemente a nivel 1,
la variable que se aplique a la otra entrada, se verá invertida en la salida,
esto ratifica la función inversor.
De igual forma nos ocurre con el producto de dos variable
invertidas que estudiamos en la función (F.1). La particularidad de un operador
NAND reside en que, si una de sus entradas se pone permanentemente a nivel 1,
la variable que se aplique a la otra entrada, se verá invertida en la salida,
esto ratifica la función inversor.