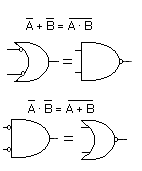LECCIÓN   1

LECCIÓN   2

LECCIÓN   3

LECCIÓN   4

LECCIÓN   5

PRÁCTICA 01

PRÁCTICA 02

PRÁCTICA 03

PRÁCTICA 04

PRÁCTICA 05

PRÁCTICA 06

PRÁCTICA 07

LECCIÓN 6

En las primeras lecciones del curso tratamos la teoría que tan necesaria se hace en la medida que nos adentramos en estos conocimientos de la lógica. Pronto descubriremos lo necesaria que se torna, para dar solución a muchos de los problemas que se presentan. 
Pero sigamos, como decía el poeta, '... se hace camino al andar'. 

En esta lección, veremos:

  Experimentos prácticos con circuitos lógicos.

  Análisis de las puertas Y.

  Análisis de las puertas NAND.

  Análisis de las puertas O.

  Análisis de las puertas NOR.

 

 
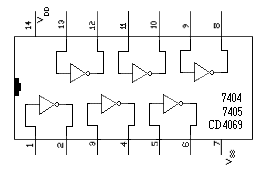
Fig. 6-1

En la figura 6-1, vemos la configuración interna del dispositivo, que dispone de 6 inversores idénticos y casualmente presenta este mismo encapsulado para los inversores especificados SN7404, SN7405 en TTL y en CMOS el CD4069, entre otros. Así pues, tomaremos un circuito integrado 4069UB (UB quiere decir, sin buffer), para nuestras próximas experiencias y una alimentación de 5V, para que nos sirva lo expuesto en el caso de que alguien sólo disponga de dispositivos TTL.

Deberíamos disponer de algún tipo de soporte, donde posicionar los componentes y los diferentes dispositivos que iremos utilizando en los sucesivos ejercicios. Dicho dispositivo debería ser reutilizable en alguna medida, si se dispone de placas preformadas del tipo prefabricadas con tiras de 'pads' para pruebas, podría servir o mejor si se puede, una placa llamada 'PROTOBOARD' similar al mostrado en la imagen de la figura 6-2.

Fig. 6-2 
 
 Fig. 6-3

Si no se puede localizar dicho tipo, uno parecido al de la figura 6-3, puede servir. En fin, la forma de ejecutar los ejemplos la dejamos un poco a la forma en que cada uno pueda proveerse del material que se necesita, el cual se describirá en cada ejercicio. 

Los componentes.

Fig. 6-4

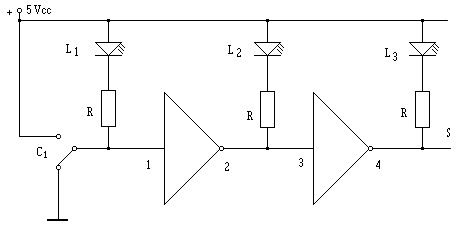
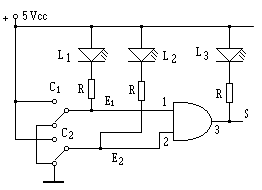
Conectemos los componentes descritos y de la forma que se aprecia en la figura 6-4. Los números 1, 2, 3 y 4 corresponden a las patillas del circuito integrado, los L₁, L₂ y L₃ son los diodos LED, las R son del mismo valor 330Ω, para limitar la corriente de salida de los inversores y evitar que se deterioren por exceso de corriente.

Ahora, teniendo el conmutador en la posición que se observa, si aplicamos la tensión de alimentación de 5V, obtendremos como resultado que los diodos LED₁ y LED₃, se encuentran encendidos, mientras que el LED₂ no lo está. Por qué se encienden de esta forma.

Analicemos la situación, en primer lugar tenemos el LED₁ el cual se enciende, debido a que por un lado está unido al +5Vcc, y por el otro lado, el conmutador está puesto a masa, está polarizado directamente, además esto nos confirma que en la entrada del primer inversor, en el pin 1, se encuentra un nivel 0, ya que como decimos está derivado a masa. Por tanto, si en la entrada de un inversor tenemos un 0, que obtendremos a su salida, naturalmente un 1 y como consecuencia de esto el LED₂  se encontrará apagado mientras permanezca esta situación, pero la acción del conmutador no acaba aquí no, porque el pin 2 y 3 se encuentran unidos y claro si uno está a 1 también lo esta el otro y, en el pin 4, tendremos como consecuencia un nivel bajo o sea, un 0 el cual de la misma manera que el conmutador hará que se encienda el LED₃ , esto confirma la teoría y es consecuencia de la inversión que se produce entre cada entrada y salida de ambas puertas. 

Cuando el conmutador cambia de posición, el LED₁ estará apagado, debido a que sus dos terminales están a la misma tensión (+5V) y el nivel aplicado al primer inversor es alto 1. Esto hace que el LED₂ se encienda, por la inversión producida, su salida esta a 0 y como dijimos antes la entrada del segundo inversor es baja, por lo tanto su salida alta y el diodo LED₃, permanecerá apagado.  

Y que podemos decir además de todo esto, sencillamente que, se produce una doble inversión y que estos dos inversores funcionan bien.  

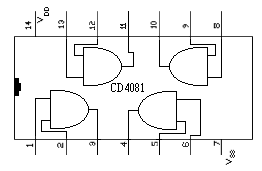
Para este experimento necesitaremos un circuito integrado con puertas Y (AND) y si es posible seguiremos utilizando uno de la familia CMOS como es el popular 4081, compuesto por cuatro puertas de dos entradas en la misma pastilla o encapsulado. Su representación se puede ver en la siguiente figura 6-5.

Fig. 6-5                                                 Fig. 6-6

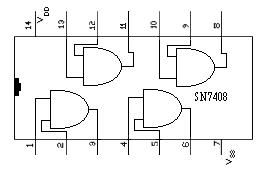
El equivalente en TTL, en funciones y cantidad de puertas es el 7408, figura 6-6, pero no es compatible pin a pin, ya que como se puede observar la disposición de las puertas con sus respectivas entradas y salidas no son iguales. Por lo tanto, si Ud. decide por alguna razón, utilizar algún dispositivo que no sea el que se describe más arriba, le aconsejamos que se asegure muy bien de qué pines va a conectar con respecto al circuito integrado que use.

Además de los componentes que hemos utilizado en la práctica anterior, y el citado circuito integrado, necesitaremos un segundo conmutador C₂ y por supuesto tendremos que conectar la puerta 1 correspondiente a los pines 1, 2 y 3, como se aprecia en el esquema de la figura 6-7.

Fig. 6-7

Mediante los conmutadores C₁ y C₂, se puede aplicar los niveles lógico 1 o 0 a cada una de las dos entradas de la puerta Y, analizando si a su salida pin 3 el nivel corresponde con lo que la tabla de verdad de la puerta Y nos indica. 

Analicemos las posibles combinaciones que podemos hacer con los dos conmutadores y veremos si se cumple la tabla de verdad de la puerta Y. En la posición inicial los  L1 y L2 están encendidos debido a que están polarizados directamente, pero además el L3 también lo esta, debido a que la salida de la puerta Y permanecerá a nivel 0, mientras que sus dos entradas no se hallen a nivel 1 simultáneamente, así pues, el L3 estará encendido, mientras esto no cambie.

Si ponemos C1 en nivel 1, L1 se apaga porque no hay paso de corriente, L2 y L3 permanecen como estaban ya que no se cumple la condición requerida para que se encienda L3. Acto seguido, devolvemos C1 a  su posición inicial y cambiamos C2 a nivel 1, que ocurre; que ahora es L2 el diodo Led que se apaga como único cambio respecto al paso anterior. En esta posición, vamos a pasar directamente C1 a la posición de nivel 1, con esto tenemos C1 y C2 a nivel 1, los Led L1 y L2 se apagan, consecuentemente la puerta Y, en su salida nos dará un nivel lógico 1 y L3 de igual forma se apagará porque sus extremos se encuentran al mismo nivel lógico y no hay paso de corriente. 

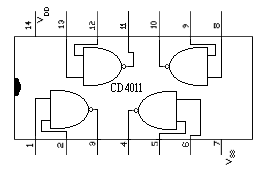
El circuito integrado (C.I.) que vamos a utilizar en esta experiencia es el popular CD4011B, un dispositivo compuesto por cuatro puertas NAND, de dos entradas cada una. La disposición de dichas puertas y su numeración, se puede contemplar en la figura 6-8.

Fig. 6-8

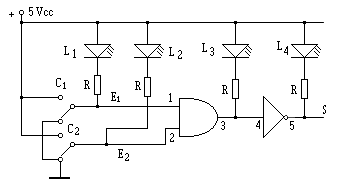
Como se puede apreciar la disposición de las puertas es idéntica a las del C.I. CD4081, salvo que éstas puertas, tienen una inversión a su salida, representada por el circulito en la salida. Empiece por anotar en un papel que tenga a mano, la tabla de verdad de una puerta NAND, para comprobar que se cumple cada una de las combinaciones que predice dicha tabla.

En primer lugar vamos a mantener el montaje de la práctica anterior del 4081, y además montaremos el 4069 detrás, para conectar un inversor de éste, a la salida de la puerta Y, formando de esta manera una puerta NO-Y (NAND). Véase la figura 6-9, para un mejor seguimiento.

Fig. 6-9

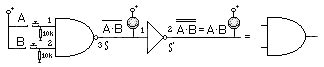
Analicemos las posibles combinaciones que podemos hacer con los dos conmutadores y veremos si se cumple la tabla de verdad de la puerta NO-Y.

En principio, podemos considerar los conmutadores C1, C2 en la posición inicial y así mismo, tanto L1 y L2 como L3 encendidos, hasta aquí ya nos es familiar pero L4 se encuentra apagado debido a la acción del inversor. Ahora, cambiamos C1 a nivel 1 y L1 se apaga  como ya vimos, todo se repite, hasta que las posiciones de C1 y C2 se encuentren a nivel 1, entonces y sólo entonces se cumple la condición que requiere la puerta Y para dar un nivel lógico 1 a su salida, esto hace que se apaguen todos los diodos led L1, L2 y L3, pero de igual modo esto hace que el inversor encienda el led L4, que pasa a ser polarizado directamente.

En la siguiente práctica veremos la versatilidad de este circuito integrado, lo que determina su gran uso por parte de los diseñadores. 

Veamos, cómo conectar dos puertas NO-Y para lograr una puerta O, para comprobar una vez más la veracidad de la teoría que vimos en la figura 5-3, de la lección 5.

Por otra parte, si revisamos la figura 5-7, vemos que con dos puertas NAND, podíamos crear un báscula R-S, pero como comprendemos que ya ha quedado claro el funcionamiento de este tipo de báscula, dejamos a discreción del lector el hacer las comprobaciones mediante la conexión de un diodo led, tanto en cada entrada R y S, como a sus dos salidas Q y Q. 

Ahora, veamos que ocurre cuando se produce una doble inversión. Si tenemos una puerta NAND seguida de un inversor, en la salida tendremos el producto de las dos entradas.  Lo que demuestra que, la doble inversión se puede considerar una anulación de la misma (como no existente), ya se vio en la figura 5-3, mediante la conexión de una segunda puerta NAND como inversor, ahora presentamos la figura 6-10, en la que se puede comprobar las combinaciones de las puertas y los niveles presentes en las salidas de las dos puertas implicadas.

Fig. 6-10

Aplicando los interruptores de las entradas A y B, según la siguiente tabla anotar los resultados obtenidos y compararlos con los de la tabla de verdad de la puerta Y.

Como ejercicio, anote en las casillas S y S' los resultados obtenidos. Estos resultados se producen en todos los tipos de puertas, por lo tanto no entraremos en los ejercicios que se sobre entiende darán los resultados según las tablas de verdad en cada caso.

En este caso utilizaremos el C.I. 4071, cuya cápsula se presenta en la figura 6-11. Ahora nos proponemos comprobar las distintas posibilidades que nos ofrece este tipo de puertas O y sus combinaciones.

Fig. 6-11

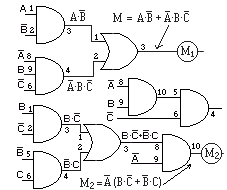
De la misma forma, si repasamos las lecciones anteriores, podemos comprobar la veracidad de los enunciados de las leyes y teoremas de la lógica que se estudio en las mismas. No vamos a comprobarlas aquí, dando por hecho que se han entendido. Si embargo, si vamos a revisar uno de los problemas resuelto.

Si recordamos el tercer problema de la lección 4, vemos que la solución que allí se obtenía consiste en una combinación de puertas AND y puertas O. Veamos de nuevo la figura 4-10, y vamos a comprobar su veracidad.

Fig. 4-10

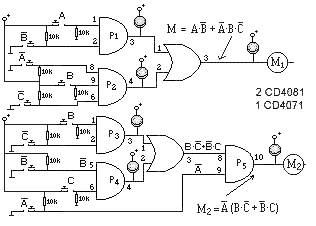
Si Ud. necesita recordar el problema, pulse este enlace. La propuesta consiste en conectar un diodo Led en las respectivas patillas 3 y 4 de las puertas Y, de las entradas correspondientes de ambas funciones, y otro diodo Led en las patillas (3 puerta O y 10 puerta Y) de cada salida, donde están M₁ y M₂, de esta forma podremos comprender mejor el funcionamiento y solución de las funciones que se describen en dicho problema, para esto necesitaremos un total de 6 diodos LED, 2 CI CD4081B y 1 CI CD4071B.

Fig. 6-12

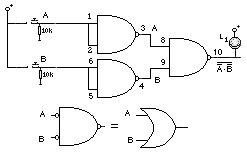
Obsérvese que se ha dispuesto una resistencia de 10k entre cada entrada y masa, de manera que en ausencia de señal, el nivel en dicha entrada sea bajo (0), así mismo se utilizan interruptores deslizantes para establecer los niveles de modo seguro. Los LED se representan sin la pertinente resistencia para controlar la intensidad, por no aumentar la densidad del diagrama, pero se entiende que la llevan. 

Así, cuando se aplica un nivel alto en la entrada A y al mismo tiempo en B negada (no se aplica, gracias a la R de 10k a positivo), en la salida P₁, obtendremos un nivel alto (1), encendiendo el LED. Lo que comporta que el Motor₁ (LED) se encienda también. Cuando cambie de situación alguno de estos dos interruptores, la salida también lo hará y se apagará el LED.

La segunda función P₂, A y C negadas cuyas entradas en estado normal se encuentran a 1 y la entrada B que se halla en 0, cuando cambiamos B a 1, la salida de P₂, pasa a nivel 1 y por lo tanto el LED se enciende. En cuyo caso activará el Motor₁ de la misma forma que en el caso de la puerta P₁. 

La segunda ecuación la dejaremos para que Ud. descubra cómo se comportan las  puertas P₃, P₄ y P₅, como ejercicio. 

Análisis de las puertas NOR.

Ahora nos proponemos realizar unos pocos ejercicios que nos ayuden con la práctica a comprender mejor lo que ya se vio en la teoría. 

El comportamiento de las puertas NOR, responde a lo previsto en su tabla de verdad y cuando se aplica una doble inversión se obtienen los resultados que previamente nos predecía la tabla de verdad al aplicarla a dicha combinación, véase la figura 6-13. El lector deberá completar los resultados esperados en la tala de más abajo correspondiente a las columnas S y S' y compruebe que los resultados del ejercicio, se corresponde con lo anotado en la tabla.

Fig. 6-13

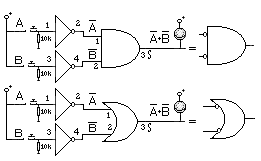
Podemos comprobar que es cierto lo que se decía anteriormente con las puertas NAND.

Veamos las equivalencias entre las siguientes puertas y constataremos el teorema de De Morgan.

Fig. 6-14

En esta figura se puede ver a la derecha el símbolo que representa estas puertas. Utilizando los interruptores de las entradas, comprobar las tablas de verdad de ambas. Obsérvese que al comparar las tablas de verdad, hay una equivalencia entre las puertas de la figura siguiente.

Fig. 6-15

De la misma forma, podemos deducir que en el caso de doble inversión en una puerta NAND, obtendremos el mismo resultado de optar por una puerta O. Veamos el ejemplo:

Fig. 6-16

En el caso de usar puertas NOR para implementar una puerta AND, obtendremos los resultados correspondientes a la tabla de verdad de la puerta Y. Dejamos al estudiante que haga su práctica y compruebe la veracidad de lo explicado.

Si alguna cuestión no ha quedado clara, deberías indicármelo en este enlace. 

Creada el:12/06/02